指定した3点を通る円の式 困っていたのでありがたいです。 計算過程も書いてあると尚嬉しいです。 タンクの中心からずれた位置へ差し込むパイプの長さを求めました。 半径rと x座標a,c,e から y座標b,d,f が求められればサイコーです! アンケートにご 更新日時 座標平面における円の方程式には以下の2つの形がある: 中心と半径による形: ( x − a) 2 ( y − b) 2 = r 2 (xa)^2 (yb)^2=r^2 (x−a)2 (y −b)2 = r2 一般形: x 2 y 2 l x m y n = 0 x^2 y^2 lx my n = 0 x2 y2 lx my n = 0 この記事では,円の方程式について解説します。これが求める円の方程式である. 中心の座標は, (a 2, b 2) ,半径は, a 2 b 2 2 となる. 内積を用いて円の方程式を導く方法は重要である. 式の導出 その2 三平方の定理を用いて方程式を導くこともできます. OQ 2 = OP 2 QP 2 より
2 つの円の位置関係 思考力を鍛える数学
円 中心 求め方 座標
円 中心 求め方 座標-ここでは, 『「円周上の点」と「中心」の距離』と『半径』が同じ ということを利用して,円の方程式を導いてみます。 さらに,この式を展開して整理すると, x2 y2 2 ax 2 by a2 b2 r2 =0 となります。 これより,円の方程式は l,m,n を定数として, x2y2lxmyn=0・・・・・・ (2) (円の方程式は, (1)や (2)の形で表されます。 ) もしかすると、こういうことですか? 例えば、円を中心点C (a,b)、半径rとすると、 円の方程式は、 (x-a)^2+ (y-b)^2=r^2なります。



外接円の方程式の求め方 数学の偏差値を上げて合格を目指す
66 第6 章 中心力のもとでの運動 面積速度 時刻t に位置r にあった質点が,微小 時間後のtΔt にrΔr に移動したとする。 微小 時間Δt のあいだに位置ベクトルが掃いた面積ΔS は,r とΔr を2辺とする三角形の面積で近似でき る(図63)。 Δr の大きさをΔr と表し,r とΔr とのなす角をVBA Tips Excel19 with Windows10 2点を通り半径Rの円の中心を求める 2点と半径から中心を求める計算式としては、「2つの円の方程式をもとに連立方程式を解くとよい」とネットで説明があったが、連立方程式はイマイチ面白くなかったので、他の方法が無いか自分で図を書いて求めてみました。 接線の方程式は求めた後なので、 円の中心と接点を通る直線の方程式を求めます。 中心の座標は分かっているので、傾きがわかればオッケーです。 接線の方程式と、円の中心と接点を通る直線の方程式は垂直に交わるので、 それらの傾きの積は-1となり
ここで求めた中心点の座標から任意のデータの座標までの線分≒半径 中心点のx座標算出とy座標算出を別々のシートで行えば可能かなと思いました。 a列にx座標が設定されていて 2行目にy座標が設定されているとして 単純に円の半径を求めるやり方にも3点で円の芯出し・測定をするプログラム 3点の座標から丸物の中心座標と半径を算出するプログラムです。 パソコンに座標を入力する必要がなく、NC設備内で計算を行い、その場で計算結果を出してくれます。 用途に応じて、下記の2種類のプログラムを用意しました。 芯出しバーなどの測定ツールを使用し、各3点の現在位置の機械座標を読み込んで計算を行う 次の円の方程式を求めなさい。 しかし、直径の両端の点の座標が分かっているから、この中点が円の中心になります。中心の座標は\ \left(\frac{5}{2},\frac{5}{2}\right) \となりますね。 三平方の定理から来ていることを考えれば、式を理解するのはそれほど
直角に回転したパスの交わるところが円の中心になっているはずです。 本当でしょうか? 選択ツールで円を選択します。 きちんと円の中心と直線パスの交差しているところが円の中心だとわかりますね。 さてここからが本題です。 球の中心の求め方 前回のコラムで3次元空間での円の中心の求め方について記述したので、次に空間内にある球の中心を求めるロジックについて考えてみます。 球については、表面上にある4点の座標が指定されたら形状が確定します。 (3点の座標と半径 2点と半径から円の中心座標を求める ごく普通に解いてみる 2点と半径で円の中心が決まるのはごく簡単です。 こんな感じですね。 さて、当然の事ながら2次方程式の解ですので答えは最大2つ出てきます。



Excelで操る ソルバーで3点を通る円を求める




数学 円の接線の方程式の求め方 解法 接点の座標も求める 高校 数学 図形と方程式 数学2 質問ありがとうございます 行間 ぎょうのあいだ 先生
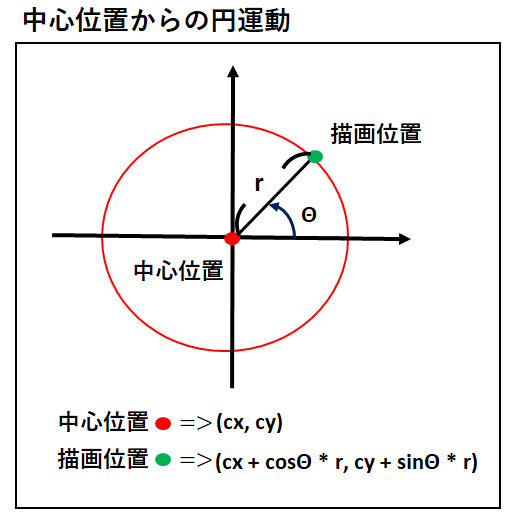
右図5において,原点を中心とする半径5の円の方程式を求めてみよう. 円周上の点 P の座標を (x , y) とおくと,ピタゴラスの定理(三平方の定理)により, x 2 y 2 =5 2 (A) が成り立つ. 上半円については, y ≧ 0 なので, y= (B) 結論から言うと、円の中心からx軸に対し、角度θの直線が円周と交わる点の座標 (x, y)は、 (rcosθ, rsinθ)と求められます。 例えば、角度θが45度の場合、座標は (7071, 70,71)、角度θが60度の場合の座標は (5000, 8660)です。最終更新日 二次元座標平面上において、 (x, y) を原点中心に反時計回りに θ 回転させた点の座標 (X, Y) は、以下の式で計算できる: (X Y) = (cos




世界一早い東大模試解説 17秋 河合オープン文系第2問 軌跡 三角関数 外心 東大に文理両方で合格した男が綴る 受験の戦略



2 つの円の位置関係 思考力を鍛える数学
中心の座標は (0 円柱や円錐を斜めに切ると楕円ができる.真横に切ったときは円になる.(円錐は,切り方によっては,「楕円」「放物線」「双曲線」になる.) 2定点 (0 , 3) , ( 0 ,−3) からの距離の和が 10 となる点の軌跡の方程式を求めなさい. =1 3点を通る円POINT 円の通る3点から中心・半径を求める一般式を導出する. 導出した式で計算フォームを作成. Excelにコピペして使えるフォーマットあり. 単純な「連立方程式」の問題ですが,一般解は少し複雑な形になります. 計算フォーム Excel用フォーマット 導出 円の方程式 円の中心 円 円の中心座標の求め方 座標 (x,y)= (0,435)と (123,238)の2点を通る半径365cmの円の中心座標の求め方を教えてください。 どうぞお願いします。 この質問への回答は締め切られまし



2点を通り半径rの円の中心を求める



円の方程式を導出から考えて理解する 高校数学の知識庫
まずは、単位円を描きます。 さっそく、90°のサイン、コサインを求めてみましょう。 回転後の点Pのx座標がcos, y座標がsin です。 座標が少し求めにくいときは 150°を例に step1 回転後のPからx軸に垂線を下ろす。 この考え方はどの角度でも使えるので身に こんにちは、ウチダショウマです。 今日は数学a「図形の性質」で習う 「三角形の内心」 について、性質の証明や基本的な使い方(角の二等分線と比)、座標の求め方や位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心に関する記事と内容がかなり似ているため、こち 中心の座標と半径を求めるためには、円の方程式を次の形に変形する必要があります。 こうすることで、中心と半径を読み取ることができます。 というわけで、円の方程式を変形していきます。 まずは、並べかえて と をまとめます。 次に と について、それぞれ平方完成していきます。 平方完成ができたら、残りモノは右辺に移行しましょう。 最後に右辺を



二次元図形における円周上の座標 X Y を求める方法を教えてくだ Yahoo 知恵袋
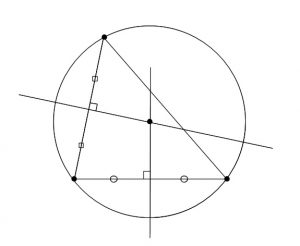



3点を通る円 と 2点とある直線上に中心がある円 の方程式の求め方
球の中心座標を機械に記憶させていきます。こ の座標値の集まりから、要素(直線、平面、円、 球など)を計算で求めます。求める要素によっ て、必要とする点の数は決まっています。例え ば、直線を求めるには最低2か所の点が必要で す。 求める円の中心は、\((−2, 0)\) と \((1, 0)\) の中点なので、 \(\displaystyle \left( \frac{−2 1}{2}, \frac{0 0}{2} \right) = \left( −\frac{1}{2}, 0 \right)\) 直径が \(3\) なので、半径は \(\displaystyle \frac{3}{2}\) ゆえに、円の方程式は \((x − a)^2 (y − b)^2 = r^2\) pYの値も解り、円の中心座標 P(pX,pY)が解るw 上記の写真を例に円の中心座標を求めてみるw A(aX,aY)=(1,1) B(bX,bY)=(5,5) C(cX,cY)=(15,5) っとしたとき、 ①②の式に当てはめてみると、 ①pX=(1^25^21^25^22pY(15))/2(15) → pX=6pY




円の中心の座標と半径を求める問題です 答えと解説を画像付きで送ってください Clear




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
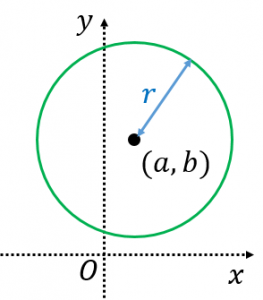
点 (a, b) を中心とし,半径が r (> 0) である円の方程式は (x − a)2 (y − b)2 = r2 中心が原点、長軸がy軸上、短軸の長さが4、点(√3,2)を通る楕円の方程式の求め方を教えてください 高校数学 方程式x^2+y^2+4x-2y=kが半径1の円を表すとき、この円の中心の座標と、定数kの値を求めよ。 という問題を教えてください! まず、3つの頂点からまでの外心までの距離は外接円の半径であり、全て同じであることに注目しました (下図の赤線は全て同じ長さ)。 すると、各頂点を中心とした3つの円の交点が外心座標であることに気付きます。 つまり、3つの円の方程式が並んだ3連立方程式を解けば外心座標を求められそうです。 { ( p x − a) 2 ( p y − b) 2 = r 2 ( 1) ( p x − c) 2 ( p y − d) 2 = r 2



Xy平面上にある斜めの楕円の円周が X軸 Y軸に接するときの 楕円の中心座標の Yahoo 知恵袋



幾何計算 2点と半径から円の中心点を求めます Satoh
こんにちは、ウチダショウマです。 今日は数学a「図形の性質」で習う 「三角形の外心(垂心)」 について、性質の証明や座標の求め方、位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心とは なぜ"外心"なのか、いきなり説明することは困難です。そこで今回は、すでに描いた円の中心点を簡単にだす方法をご紹介させていただきます。 円の中心点を簡単に出す方法 今回使用するJw_cadの便利な機能は『 クロックメニュー 』という機能です。 まずは、キャプチャー動画で操作手順をご確認ください。 円周上の座標を計算して 要素を配置する CSS JavaScript 演算 Copied!




円の方程式と関連問題 座標 ベクトル 複素数 高校数学の美しい物語




三角形の重心の座標の求め方とその証明 数学ii By ふぇるまー マナペディア
円の性質 弦と弧 円周と2 点で交わる直線を割線という。 このときの交点を 2 点 a, b とするとき、円周によって、割線から切り取られる線分 ab のことを弦といい、弦 ab と呼ぶ。特に円の中心を通る割線を中心線という。中心線は円の対称軸であり、円の面積を 2 等分する。Mathcos ( θdadian ) ある角度 θのときの x座標 を示す Mathsin ( θdadian ) ある角度 θのときの Y座標 を示す 円周上の座標は上の関数を使うことで計算できる 角度が度の時の x座標 => leftの値 , Y座標 => topの値 のようにcssで指定することで 円周上に要素を配置できる このとき引数には角度をradianとい④No12以降の各中心杭までの弧長は、中心杭間距離000mを逐次加えて求め、それに対する偏 角は、中心点杭間距離に対する偏角δを、加えることにより求める。 例えば、No12の杭は、 ° ¢ ² ° ´ ´ = 5 43 57 314 180 2 m 000m δ= であるから、IPから




高校数学 円と直線の位置関係の分類 映像授業のtry It トライイット




外心とは 三角形の外心の座標 位置ベクトルの求め方や性質の証明をわかりやすく解説 垂心 遊ぶ数学
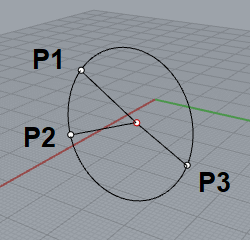
分かっている3点の座標があるとき その3点を通る円の中心座標の計算式を教えていただきたい 3点の座標がこれとします P1> x1,y1 P2> x2,y3 P3> x2,y3 円の中心の座標は P0> x0,y0 P0を求めたいです



幾何計算 2点と半径から円の中心点を求めます Satoh
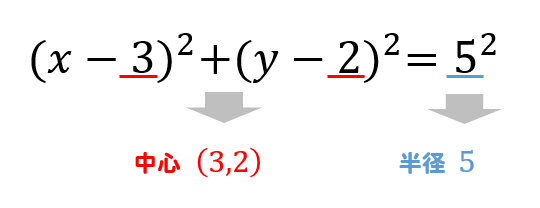



円の方程式 中心の座標と半径の求め方を解説 数スタ



3次元空間での円の中心の求め方 Inak Engineering Llc
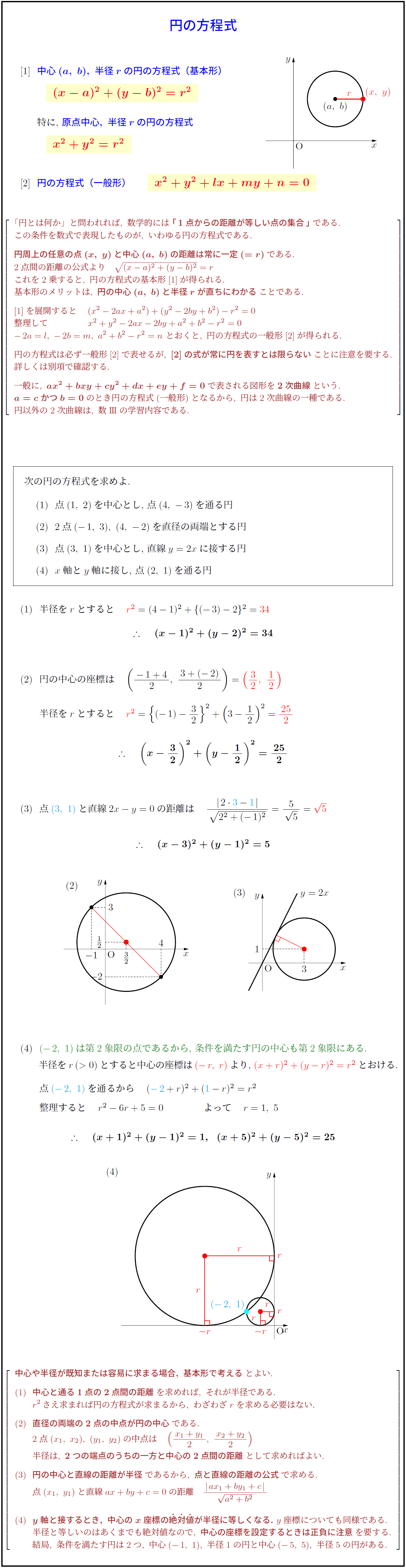



高校数学 円の方程式の基本形と一般形 座標軸と接する円 受験の月



円の方程式の公式は 3分でわかる意味 求め方 証明 3点を通る円の方程式
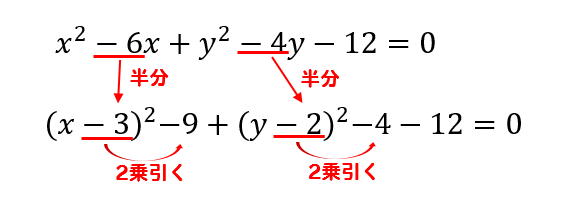



円の方程式 中心の座標と半径の求め方を解説 数スタ



Excelで操る ソルバーで3点を通る円を求める




四角形の中心の求め方 四角形の中心 真中 の求め方は 各辺の真中を 数学 教えて Goo



円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典
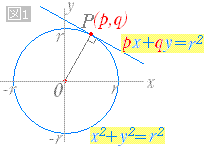



円の接線の方程式



三平方の定理で座標上の2点間の距離を求める3つのステップ Qikeru 学びを楽しくわかりやすく




空間上の測定された点群から最小二乗法により円 中心 直径 を算出す 数学 教えて Goo
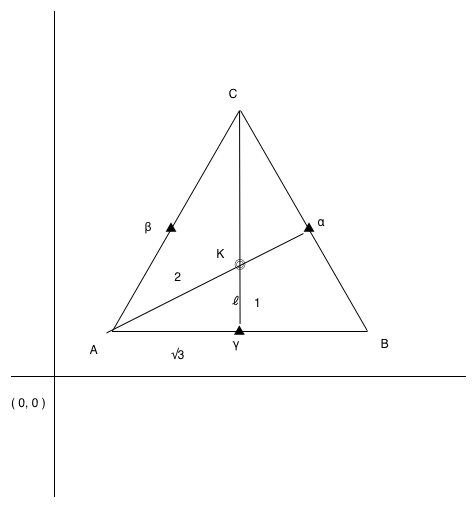



正三角形の中心座標を求める 永遠日誌




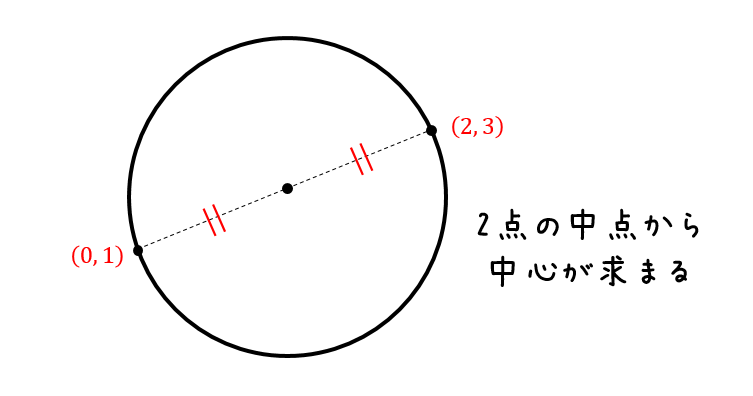
2つの点から円の方程式を求める 数学ii By Okボーイ マナペディア



1
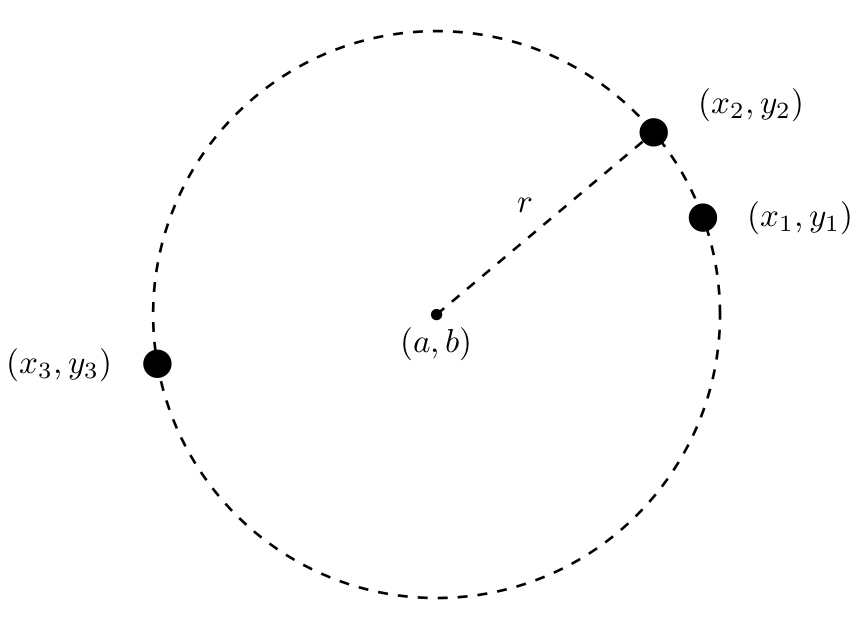



3点を通る円の中心と半径 Notes Jp




06 号 3次元位置入力装置 Astamuse
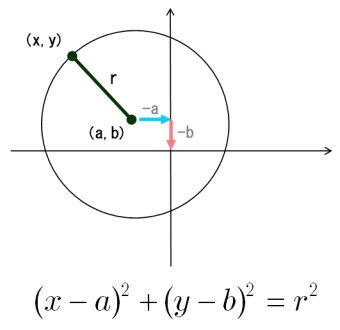



初等幾何 円の方程式 原点に中心がない場合 大人が学び直す数学



外接円の方程式の求め方 数学の偏差値を上げて合格を目指す



幾何計算 2点と半径から円の中心点を求めます Satoh
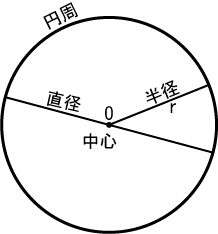



円 数学 Wikipedia




2円 円弧 に接する内接円の中心座標の求め方 Okwave



3次元 座標 数学 高校



ゲーム 円運動




基本 円の方程式 なかけんの数学ノート




9の 1 の問題の軌跡の求め方についてですが なぜこの答えの過程 黄色く囲んだ部分 Clear
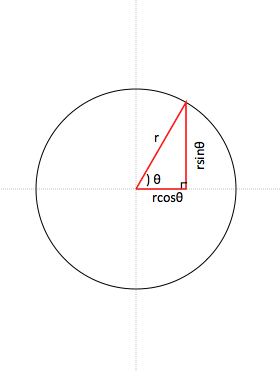



円の中心からの角度から真円の円周上の座標を計算する Gamesprit




外心とは 三角形の外心の座標 位置ベクトルの求め方や性質の証明をわかりやすく解説 垂心 遊ぶ数学



48s96ub7b0z5f Net En Hobutsusen
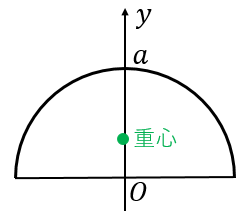



半円の重心の位置を求める公式 具体例で学ぶ数学
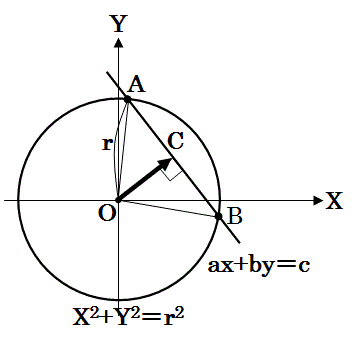



勉強しよう数学 円 半径r と直線の交点をベクトルで解く
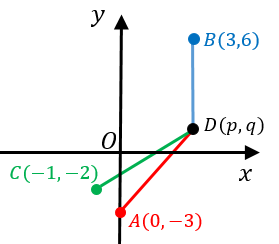



3点を通る円の方程式の2通りの求め方と検算方法 具体例で学ぶ数学



無料アプリ 株式会社キャドテック
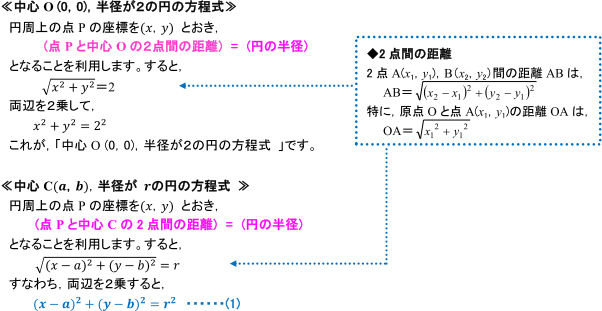



円の方程式の導き方 数学 苦手解決q A 進研ゼミ高校講座




円の弧長 弦長 矢高 半径のどれか2つを与えて残りを計算 高精度計算サイト
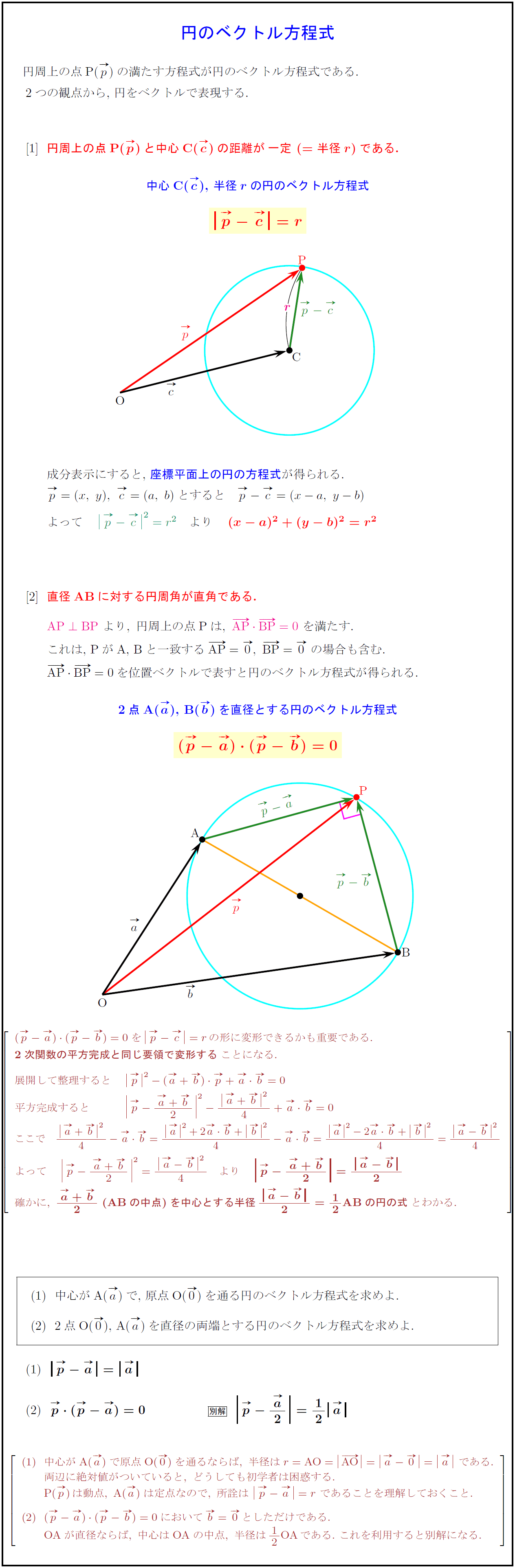



高校数学b 円のベクトル方程式2パターン 受験の月




円と直線の関係 判別式と点と直線の距離 高校数学の知識庫




2つの円の位置関係と共通接線の求め方 図形と方程式 2




三角形の内接円の方程式の求め方 数学の偏差値を上げて合格を目指す
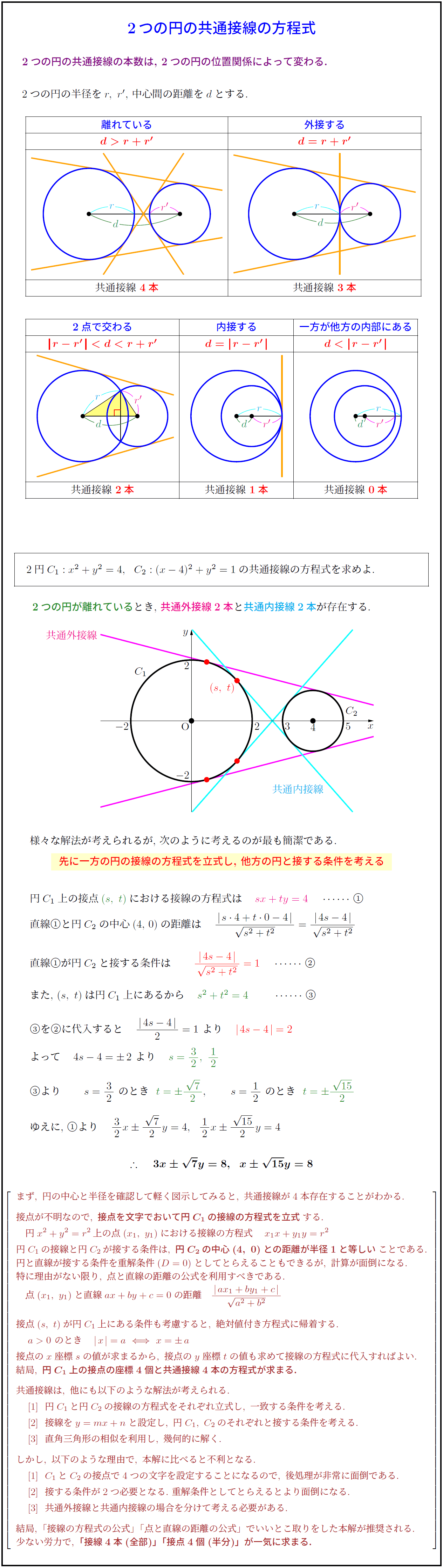



高校数学 2つの円の共通接線の方程式 受験の月




基本 2つの円の共有点 中心間の距離に注目 なかけんの数学ノート



48s96ub7b0z5f Net En Tyokusen Ten



円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典



座標計算 電卓ソフト 2次元camの新定番 かんたんキャメスト 株式会社エリジオン




三角形の内心とは 内心の意味や座標 ベクトルの求め方を解説




任意の3点を通る円を求める方法 プログラマーのメモ書き



幾何計算 2点と半径から円の中心点を求めます Satoh
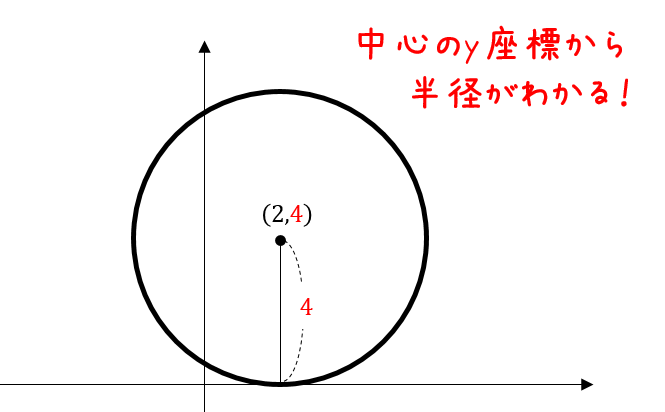



円の方程式の求め方まとめ パターン別に解説するよ 数スタ
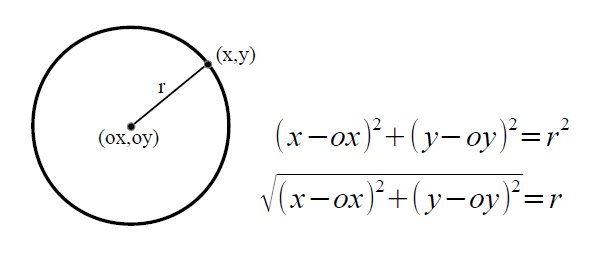



点が円内かを判定 ゆるゆるプログラミング




高校数学 三角形の重心公式 映像授業のtry It トライイット



点から円への接点を求める Qiita




円の方程式 円に内接する三角形の外心の座標を求める問題 数学ii By ふぇるまー マナペディア



3




例題付き 重心って何 重心の求め方から応用問題まで徹底解説 受験スタイル



円の方程式の求め方まとめ パターン別に解説するよ 数スタ



円 放物線との交点 中学から数学だいすき




Processing 2点を通る直線と円の交点を求めよう Zawaworks S Diary



円の方程式 公式




画像にある各座標の求め方について こちらの図で 点a B Cの座標の求め Okwave
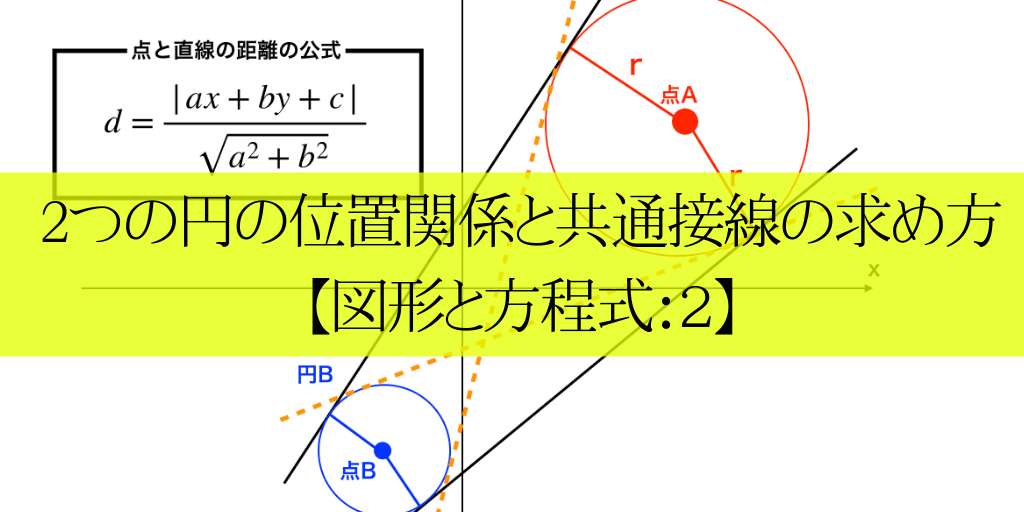



2つの円の位置関係と共通接線の求め方 図形と方程式 2
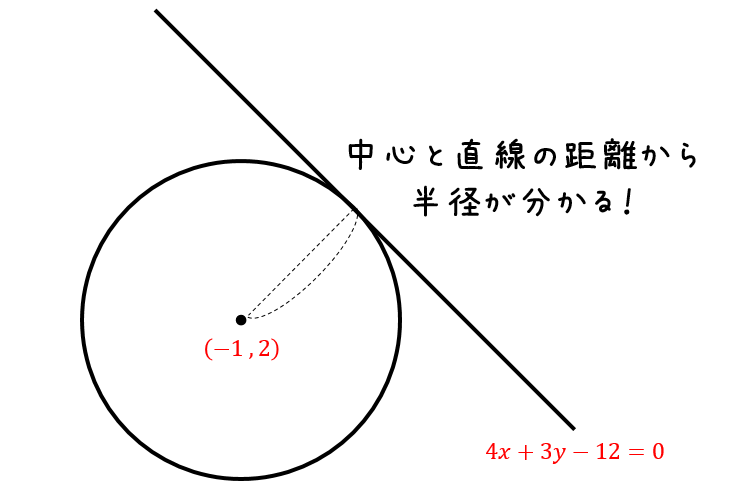



円の方程式の求め方まとめ パターン別に解説するよ 数スタ



1
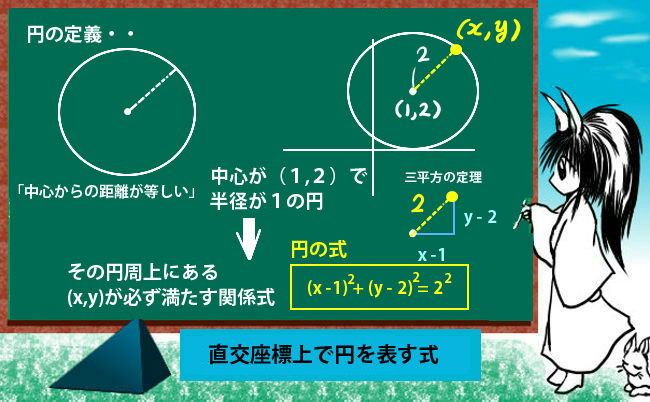



円を表す式 直交座標 理数系無料オンライン学習 Kori




勉強しよう数学 3月 11




円の方程式 数学ii フリー教材開発コミュニティ Ftext




円運動の公式まとめ 運動方程式 加速度 遠心力 向心力 理系ラボ



円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典




垂直二等分線を使って円の中心をもとめる 中学数学 By Okボーイ マナペディア
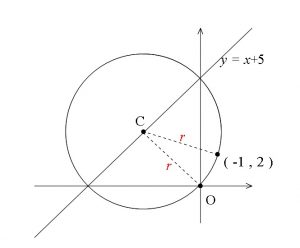



3点を通る円 と 2点とある直線上に中心がある円 の方程式の求め方




円の方程式の求め方まとめ パターン別に解説するよ 数スタ




中点の座標の求め方 中学1年数学 Youtube




円の中心の座標と半径を求める問題です 答えと解説を画像付きで送ってください Clear
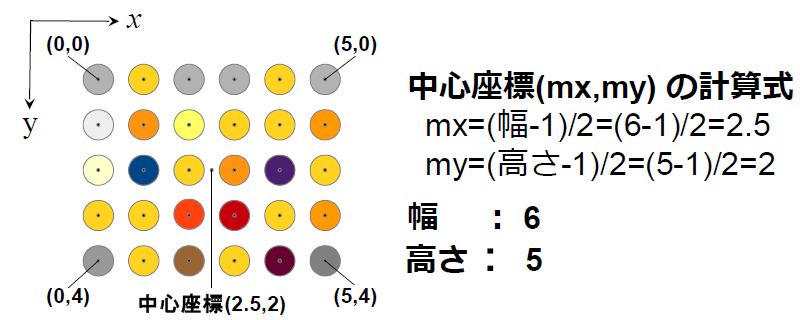



画像の中心座標 ゆるゆるプログラミング




例題付き 重心って何 重心の求め方から応用問題まで徹底解説 受験スタイル




三角形の外接円の半径と中心座標 外心 を求める Qiita



円の方程式の求め方と例題4問 具体例で学ぶ数学




球の中心の求め方 Inak Engineering Llc




3点を通る円を求める Qiita
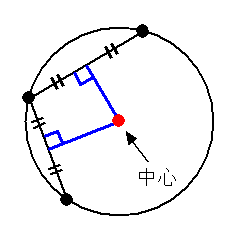



3次元空間での円の中心の求め方 Inak Engineering Llc
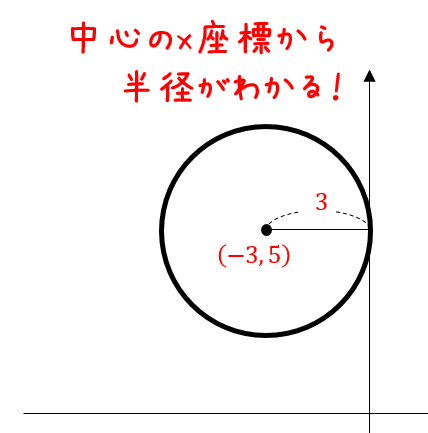



円の方程式の求め方まとめ パターン別に解説するよ 数スタ




3分でわかる 点と直線の距離の公式の証明 使い方のコツを分かりやすく 合格サプリ
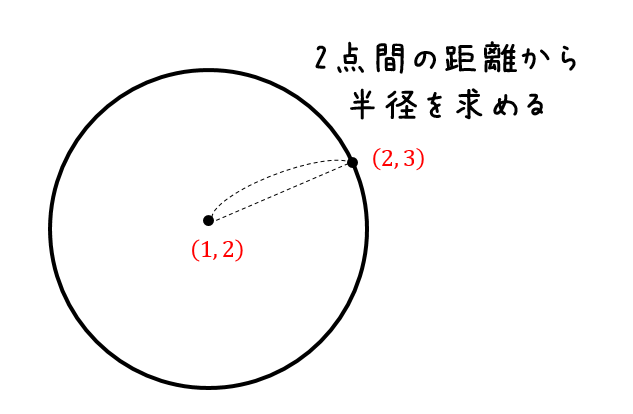



円の方程式の求め方まとめ パターン別に解説するよ 数スタ



中点と三角形の重心の座標の求め方 思考力を鍛える数学




Processing 2点を通る直線と円の交点を求めよう Zawaworks S Diary




球面の方程式の求め方と問題の解き方をわかりやすく



円の方程式の公式は 3分でわかる意味 求め方 証明 3点を通る円の方程式
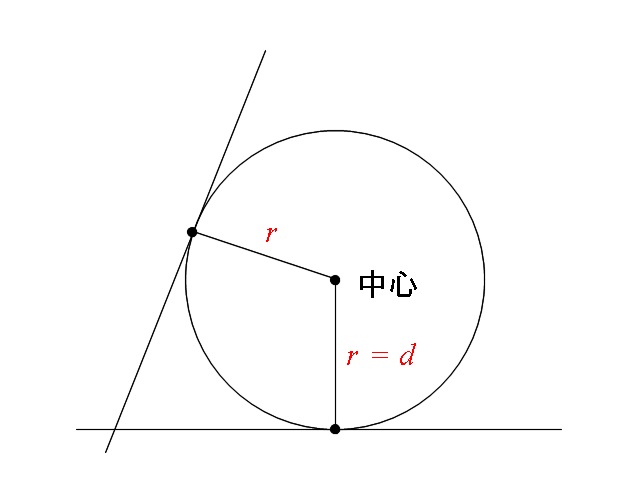



円に接する直線 接線の方程式 の求め方3パターン




重心とは何か 座標を使って重心を求める方法 物理 高校生向け受験応援メディア 受験のミカタ



0 件のコメント:
コメントを投稿