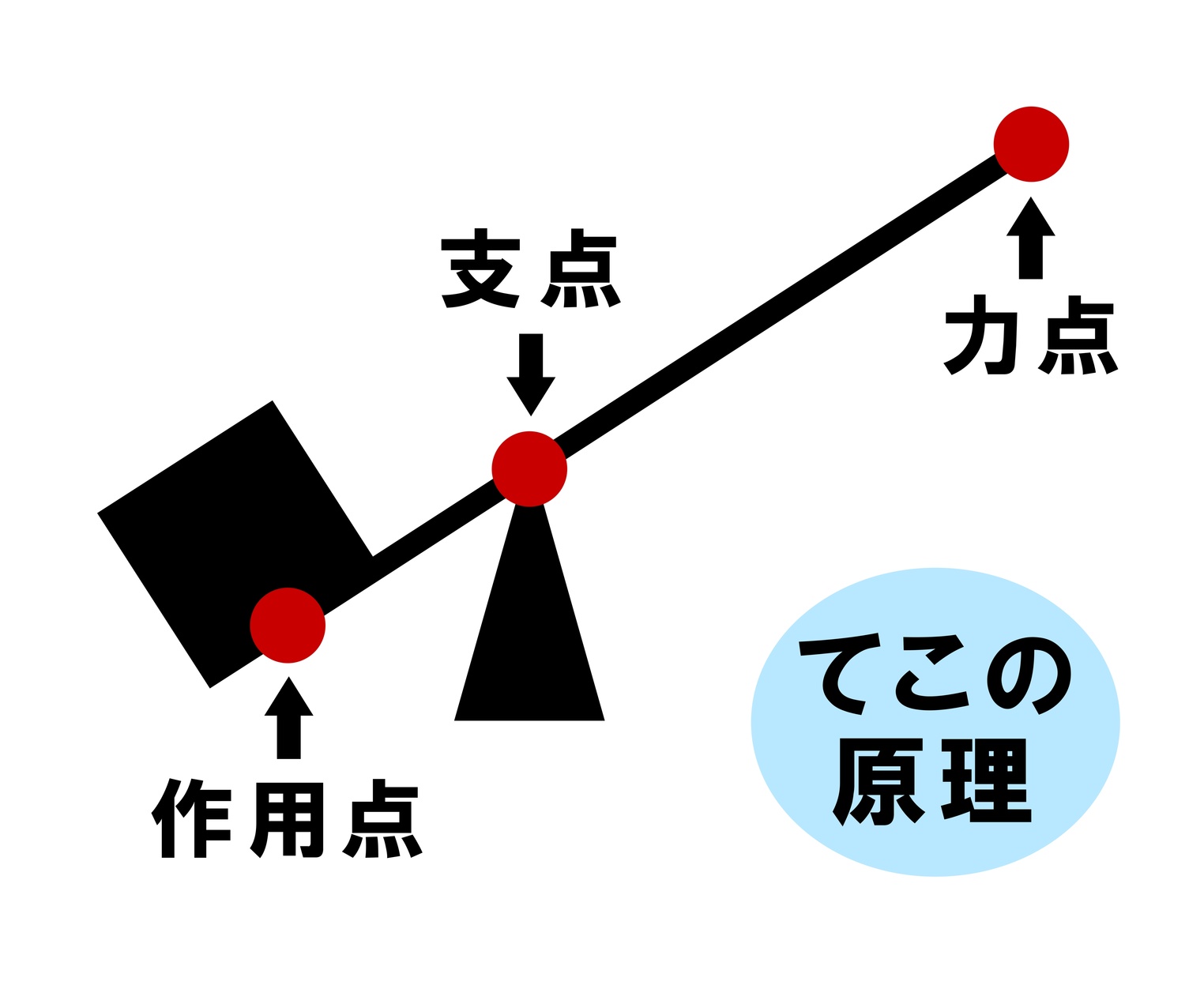
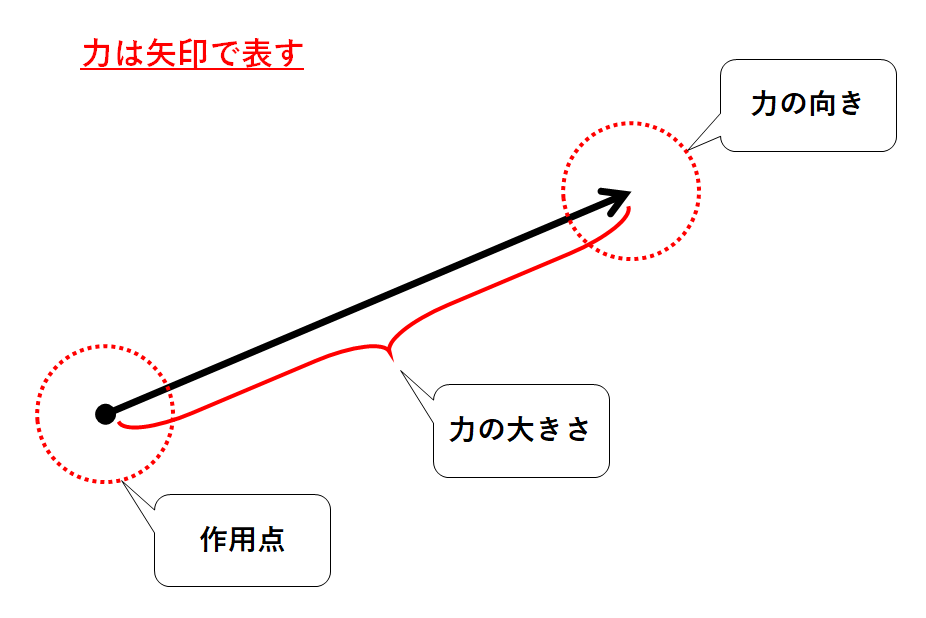
てこの原理とは 計算方法や 問題を解くための 王道アプローチ を紹介 中学受験ナビ
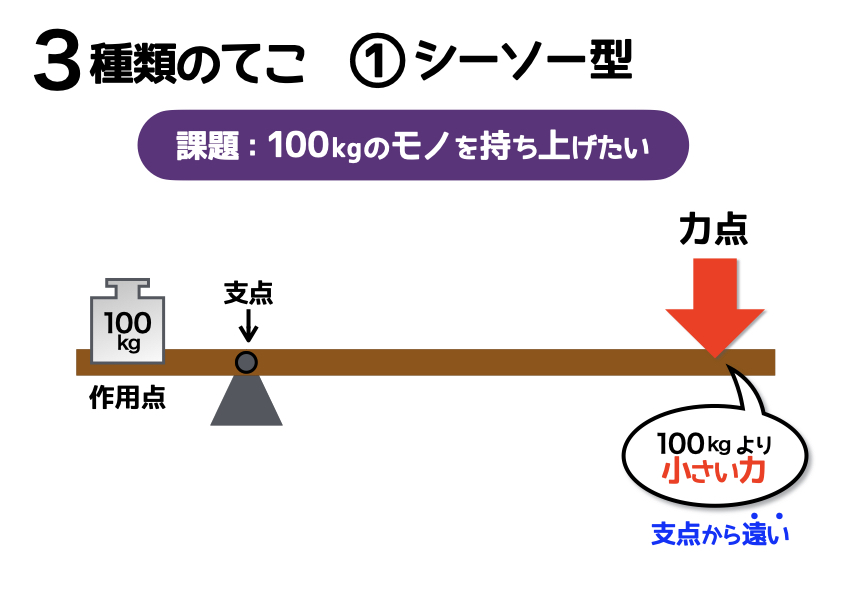
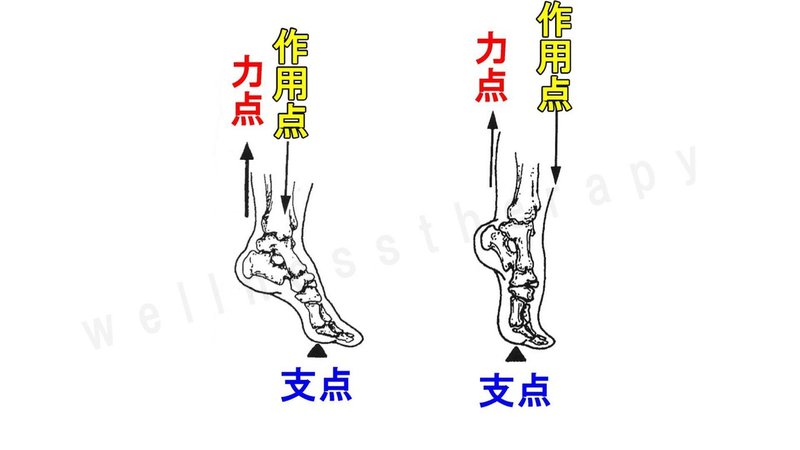
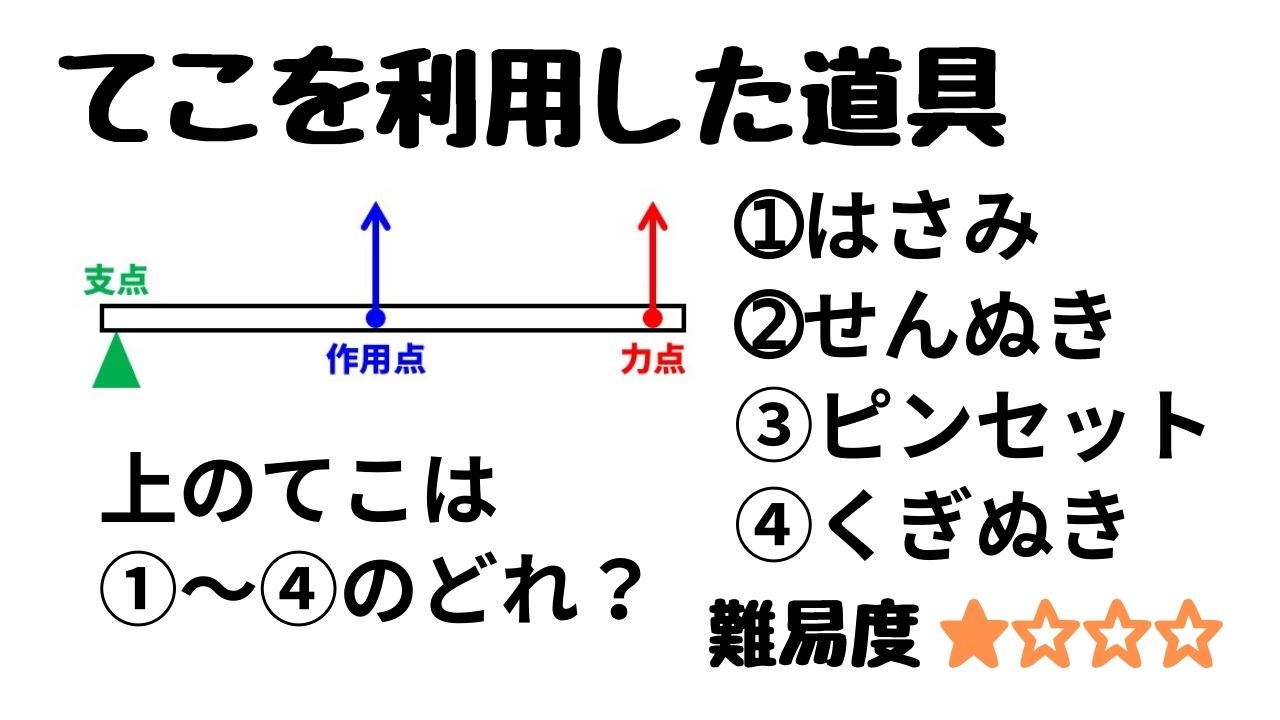
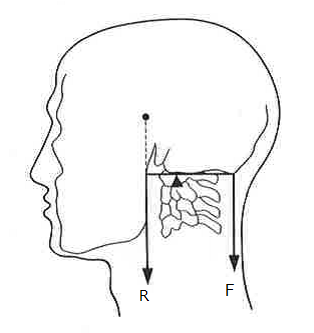
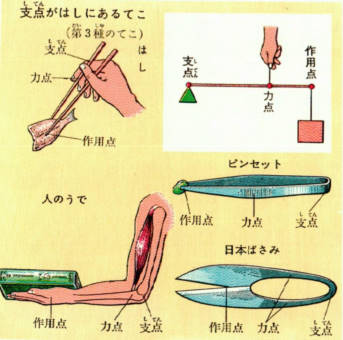
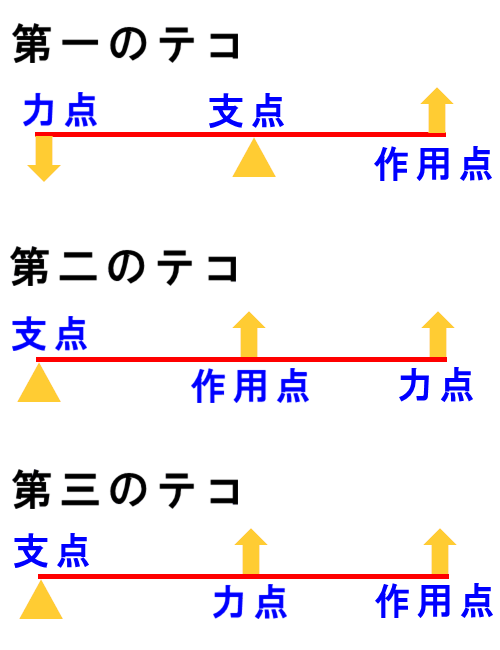
支点と作用点のあいだを短く 支点と力点のあいだを長くすると、小さい力で大きな力がでます。 てこの利用とその特徴とは？ 支点の位置よる特徴とは？ 科学をわかりやすく解説力点が支点と荷重点の間にあるてこです。特徴は 「運動の速さに対して有利」 ですが，一方で 「力に対しては不利」 であることです (詳しくは「てこの力学的有意性」を参照して下さい)。人体で作用するてこの多くはこの第3のてこです。
支点力点作用点 わかりやすく
支点力点作用点 わかりやすく-支点とは 物を静止させ安定させる支持点であると同時に そこを中心に 回転運動を支える点でもある。 肩の回転と腕の振りによって スイング軌道の位置が決まるゴルフスイングで その安定性と精度を高めるためには 肩の回転の支点と回転体の重心に注目 滑車の問題は、一見ややこしく見えます。しかし、仕組みさえ理解できればスムーズに解けるようになるものです。この記事では、定滑車と動滑車を組み合わせた問題を解ける力をつけることを目指します。 定滑車ってなに？ 定滑車は固定された滑車 定滑車の支点・作用点・力点 定滑
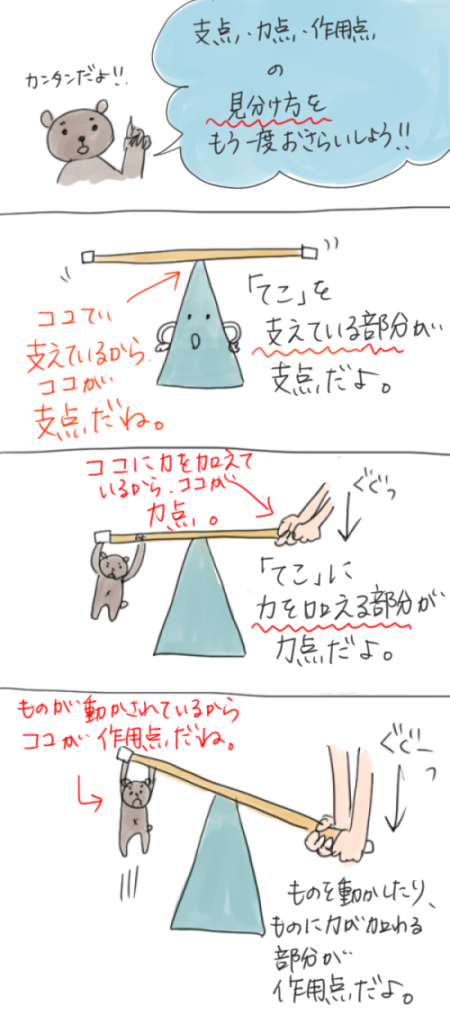
てこのはたらき 小学6年生理科を漫画で学習 てこを利用した道具 教科書をわかりやすく通訳するサイト
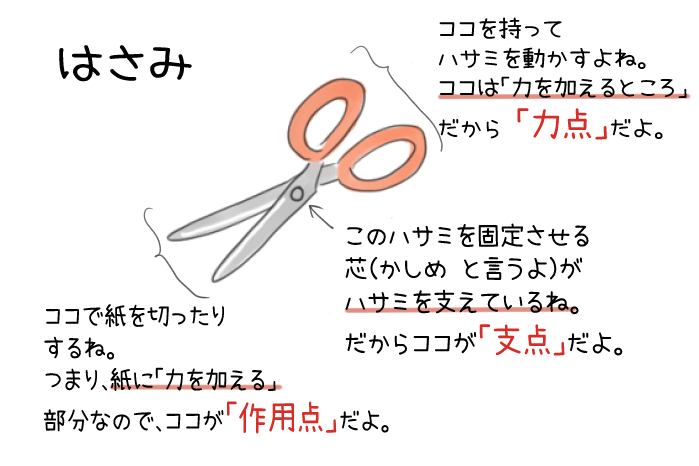
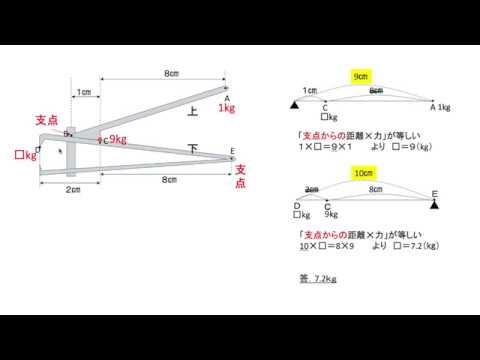
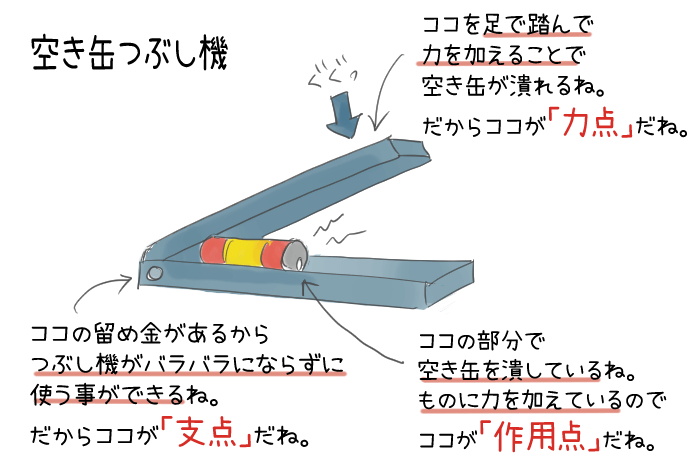
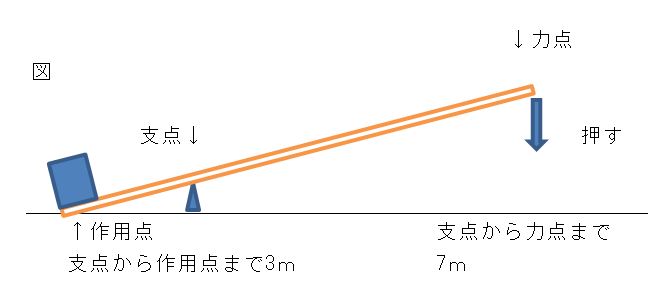
作用点での力の大きさ×支点から作用点までの距離＝力点の力の大きさ×支点から力点までの距離 という法則は同じです。 くるみ割り器や蓋のオープナーはこの原理が使われています 小さい力でも 大きな力で掴んだり、押し付けることが出来ます。 支点力点作用点は上の画像のようになっています。これを見てもハサミがてこの原理を応用していることをなかなか納得できないかもしれません。 もう一度、てこの原理の基本に戻ってみましょう。 熱力学第二法則を宇宙一わかりやすく作用点にも上向きの力がはたらいている。 このように，支点一作用点－カ点の順に ならんだてこでも，支点と力点までのきょ りが長いほど，小さい力でものを持ち上げ おさ ることができる。同じように，支点と作用 点ときょりが短いほど，小さい力で
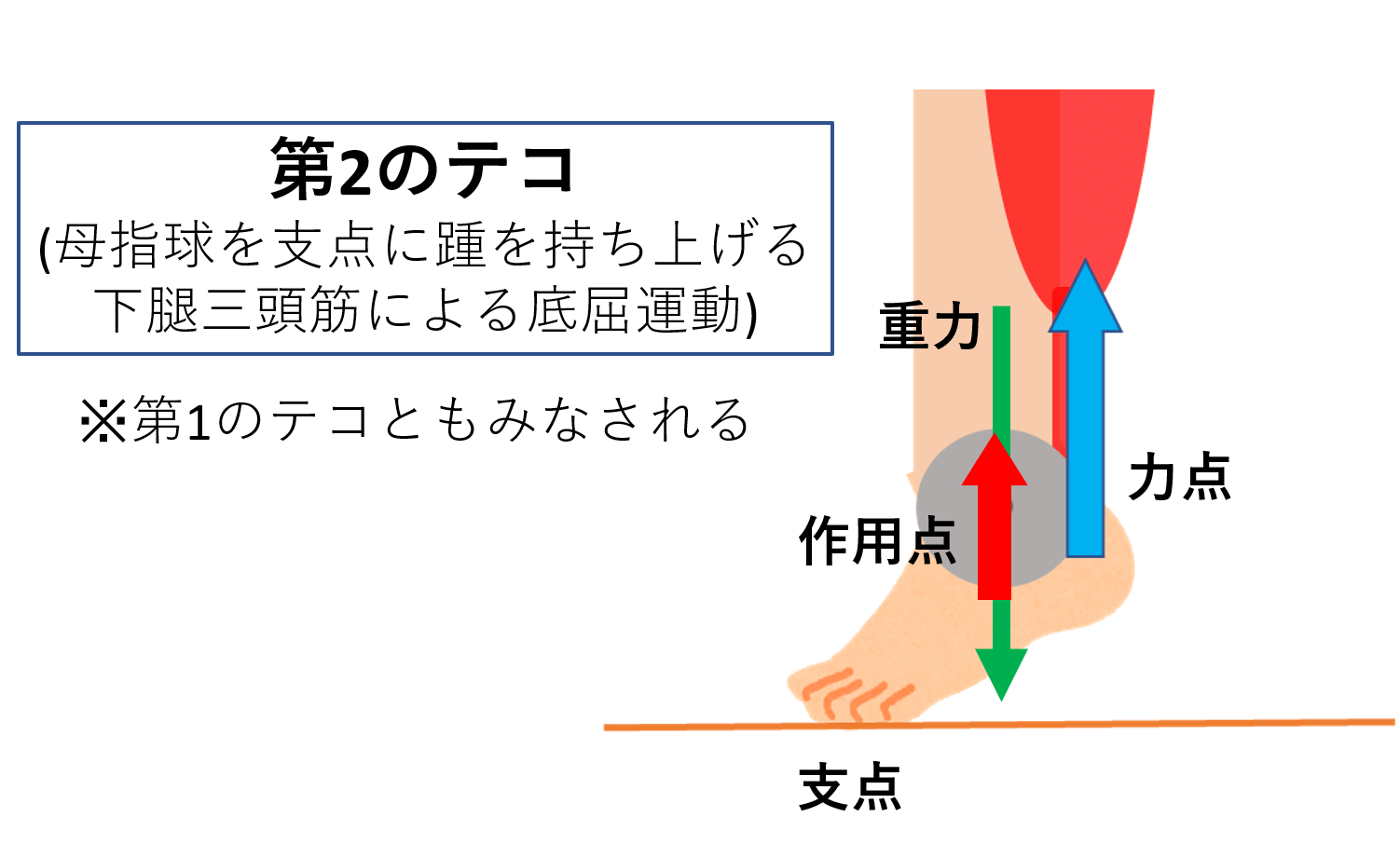
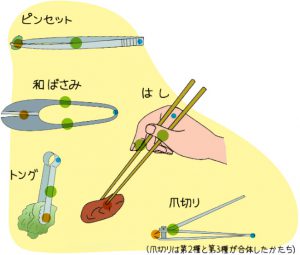
支点から作用点までの距離のほうが、力点までの距離よりも長くなっています。 これが、第三種テコの特徴です。 下の図で言えば、支点は右端。つまり、 支点を中心として最も大きな運動を得ることができます 。しかし、その反面、力点に必要な力は、第5 力のモーメントは外積式で表され る M モーメントNm r モーメントアームm F 力N M = r ×F 力の作用線 r A 回転軸 H θ Fcosθ Fsinθ F O θ 力の垂直成分Fsinθによって回転が生じる Fsinθ最大：θ＝90°のとき、モーメント最大 θ＝0°，180°のとき、モーメントはゼロ→並進運動 yumineko / てこが使われている道具一覧をイラストで紹介！ ホッチキスやはさみ、クリップ・・身の回りにある「てこを利用した道具」の力点・支点・作用点をそれぞれをイラストを使って一覧にまとめました。
支点力点作用点 わかりやすくのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 | 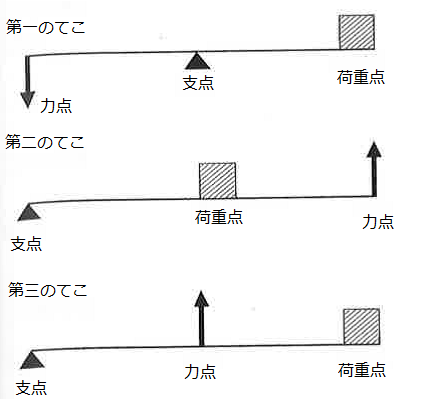 てこの原理を用いた計算方法 公式と問題 |
 てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |
 てこの原理を用いた計算方法 公式と問題 | 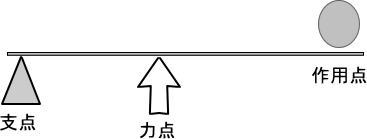 てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |
「支点力点作用点 わかりやすく」の画像ギャラリー、詳細は各画像をクリックしてください。
てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |
てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |
 てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |
「支点力点作用点 わかりやすく」の画像ギャラリー、詳細は各画像をクリックしてください。
 てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |
 てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 | てこの原理を用いた計算方法 公式と問題 |
 てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |
「支点力点作用点 わかりやすく」の画像ギャラリー、詳細は各画像をクリックしてください。
てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |
 てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 | てこの原理を用いた計算方法 公式と問題 |
 てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |
「支点力点作用点 わかりやすく」の画像ギャラリー、詳細は各画像をクリックしてください。
 てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 | てこの原理を用いた計算方法 公式と問題 |
てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 | てこの原理を用いた計算方法 公式と問題 |
 てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |
「支点力点作用点 わかりやすく」の画像ギャラリー、詳細は各画像をクリックしてください。
 てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 | てこの原理を用いた計算方法 公式と問題 |
 てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |
 てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |
「支点力点作用点 わかりやすく」の画像ギャラリー、詳細は各画像をクリックしてください。
 てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |
てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |
 てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |
「支点力点作用点 わかりやすく」の画像ギャラリー、詳細は各画像をクリックしてください。
 てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |
てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |
 てこの原理を用いた計算方法 公式と問題 | てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |
「支点力点作用点 わかりやすく」の画像ギャラリー、詳細は各画像をクリックしてください。
 てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |
 てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |
 てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |
「支点力点作用点 わかりやすく」の画像ギャラリー、詳細は各画像をクリックしてください。
 てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |
 てこの原理を用いた計算方法 公式と問題 | てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |
 てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |
「支点力点作用点 わかりやすく」の画像ギャラリー、詳細は各画像をクリックしてください。
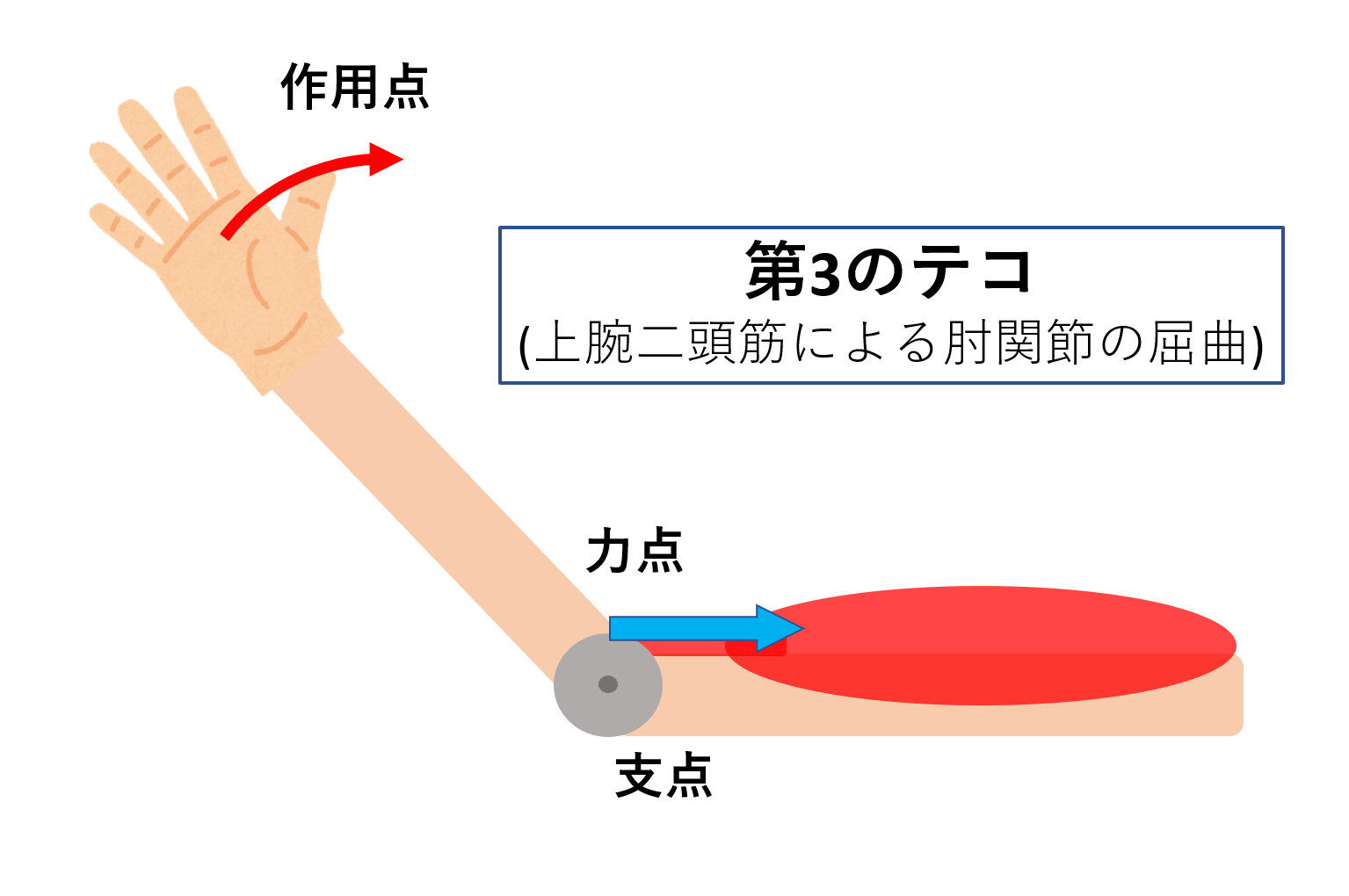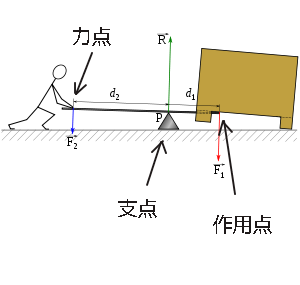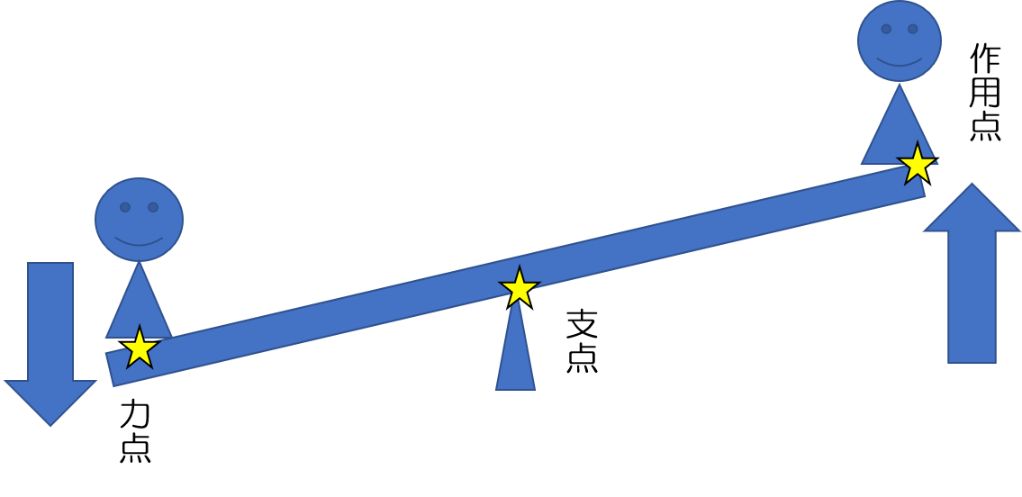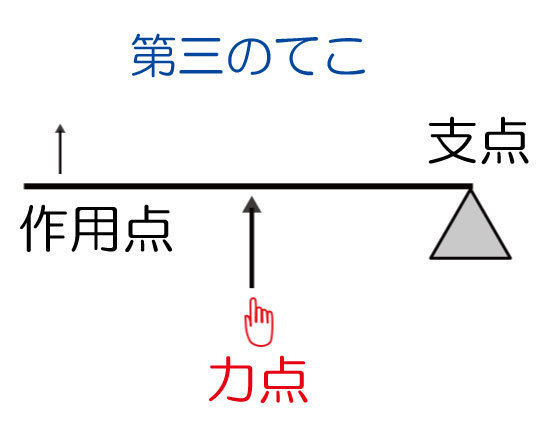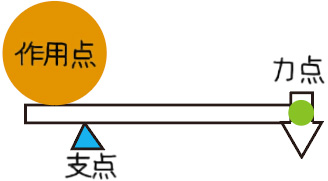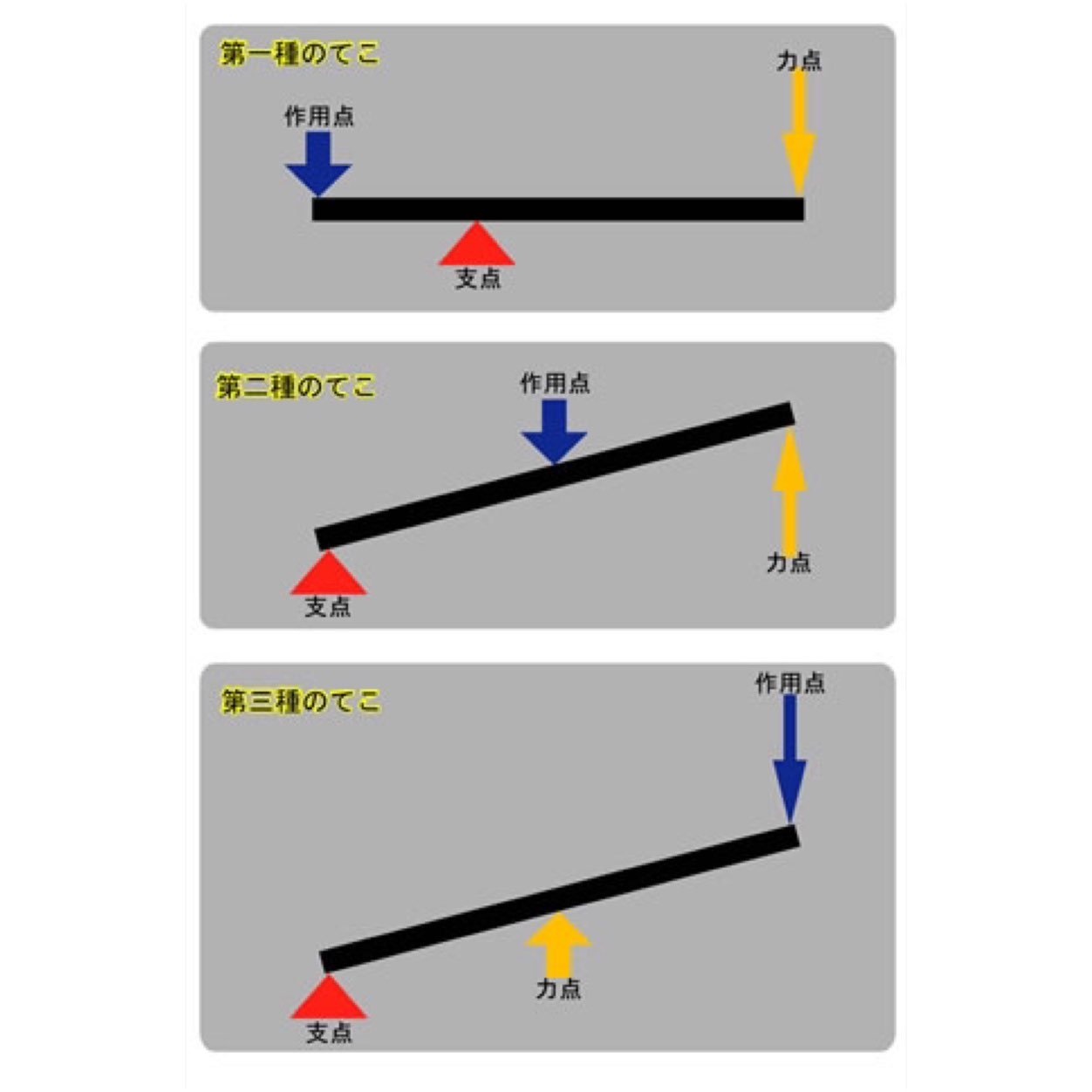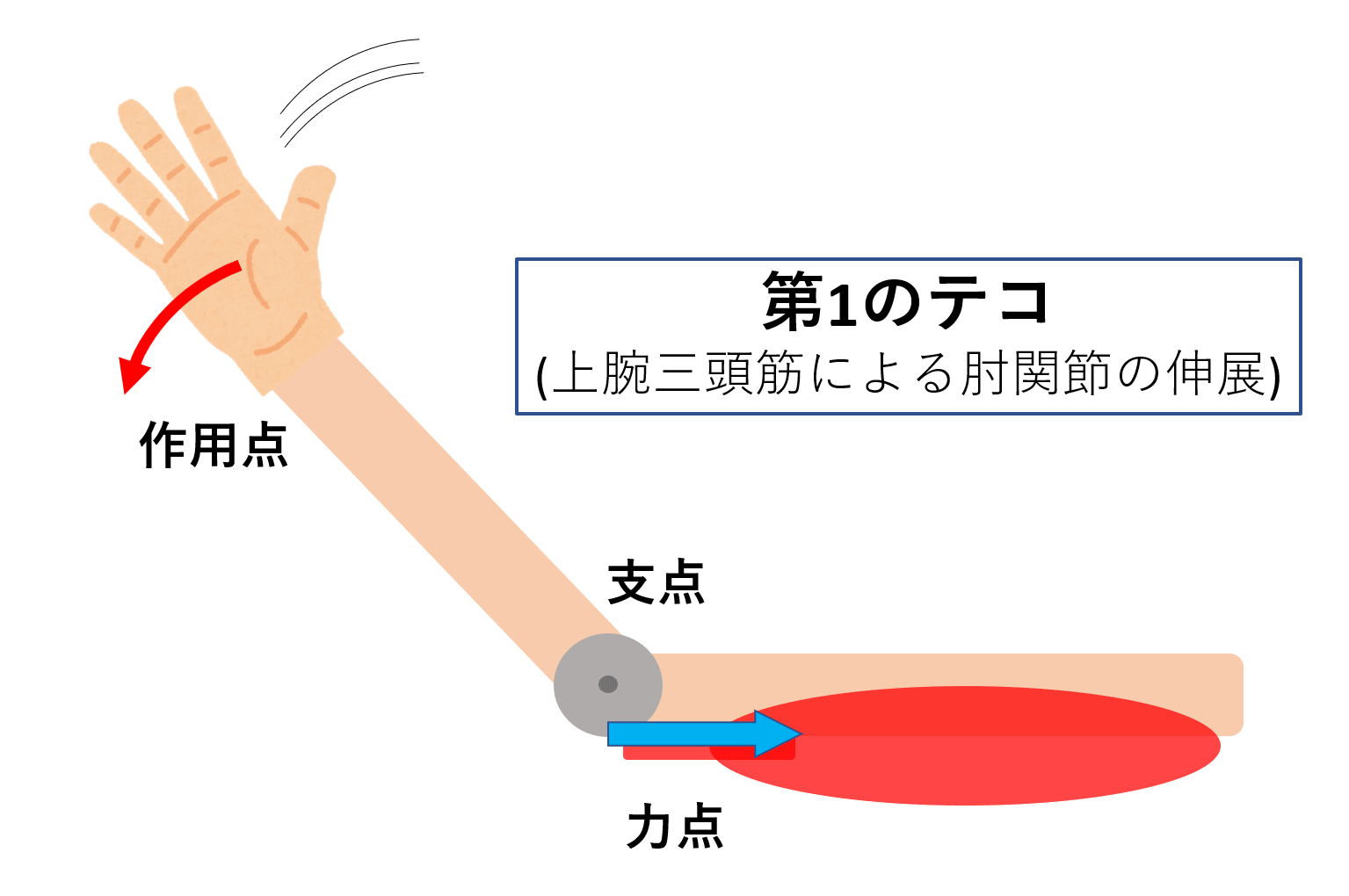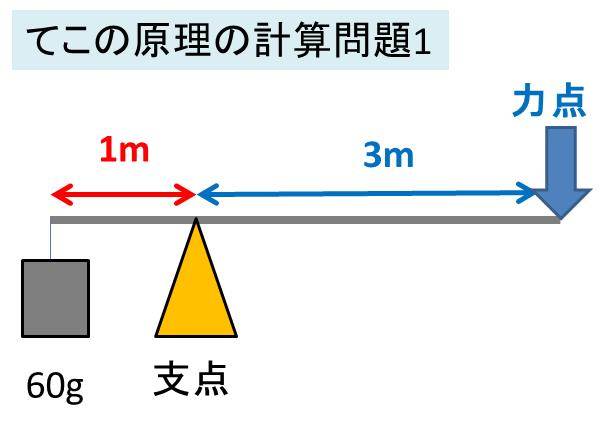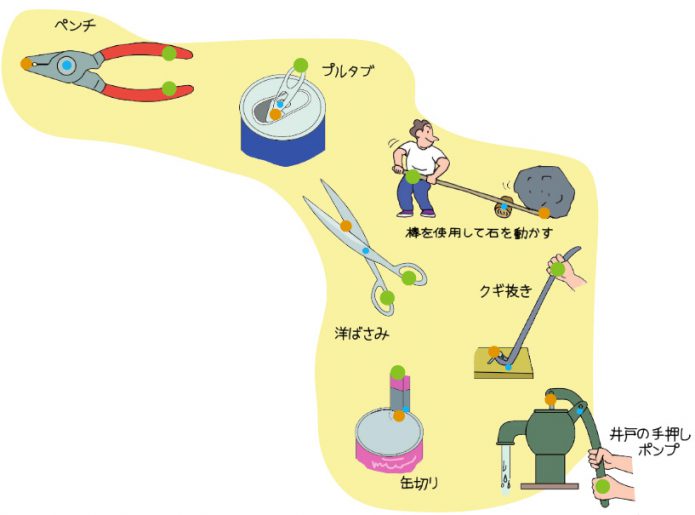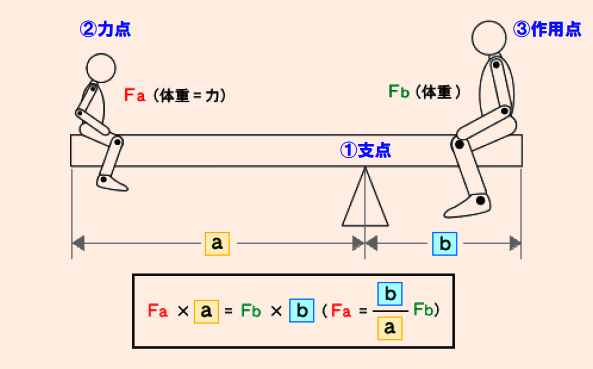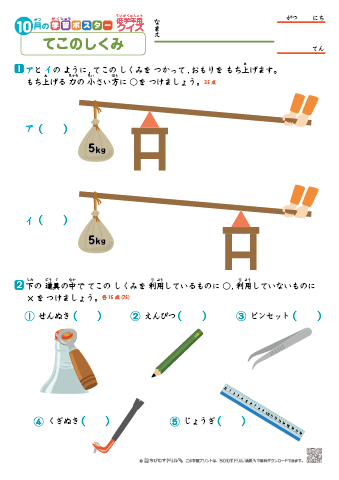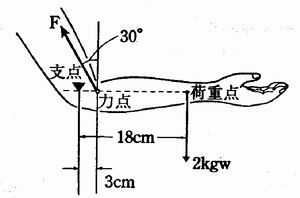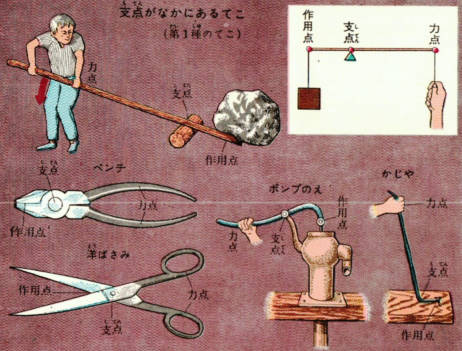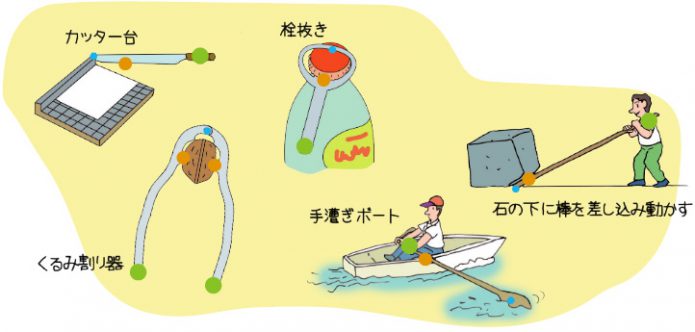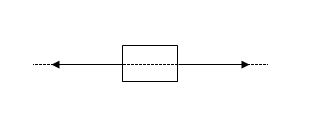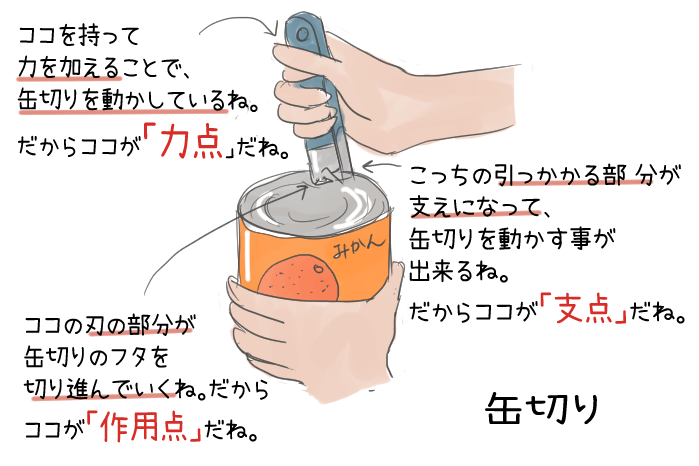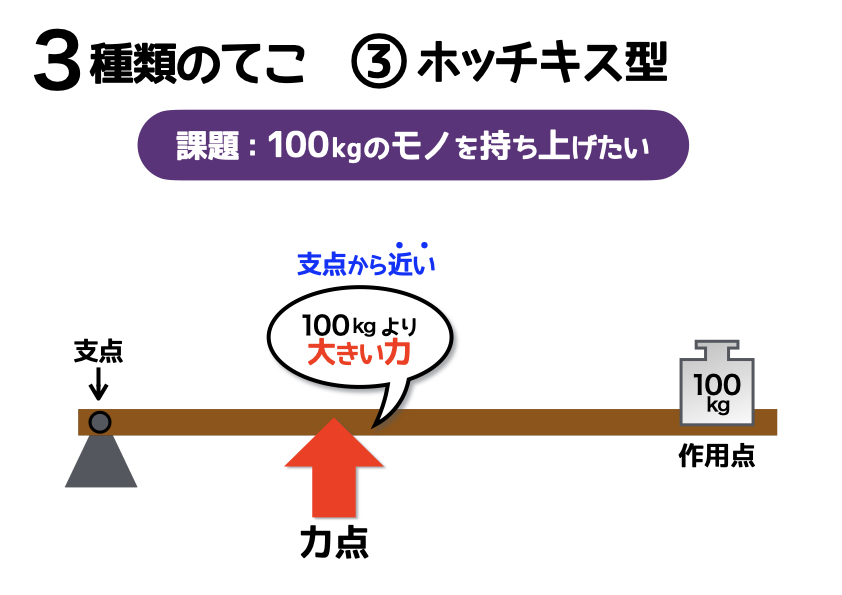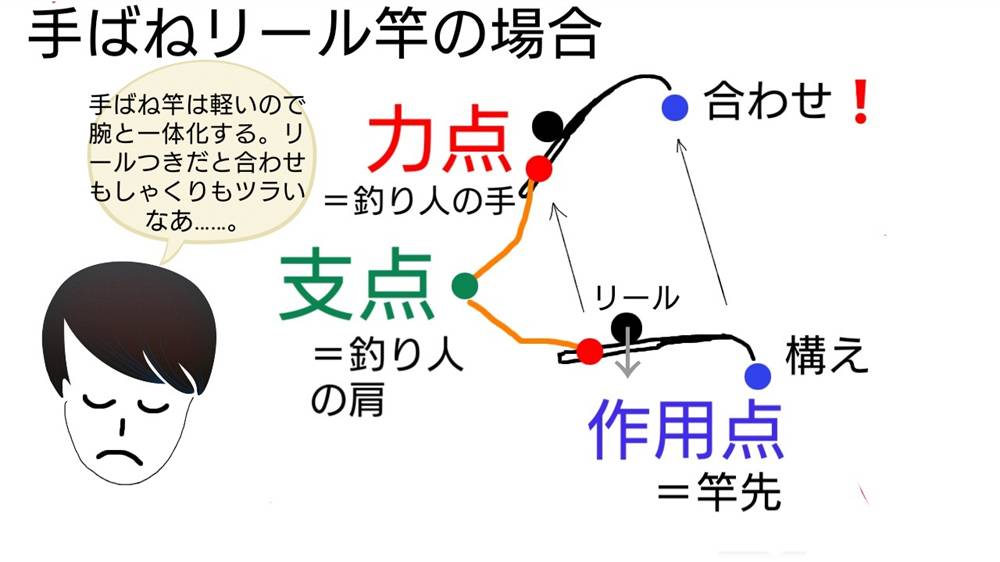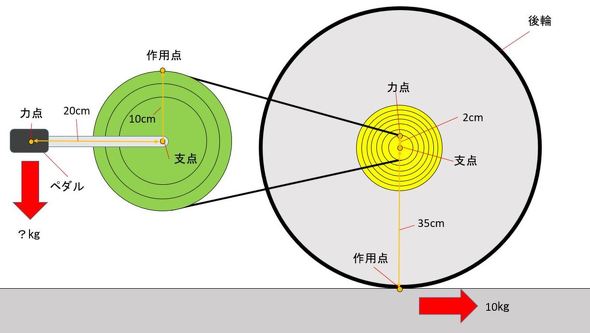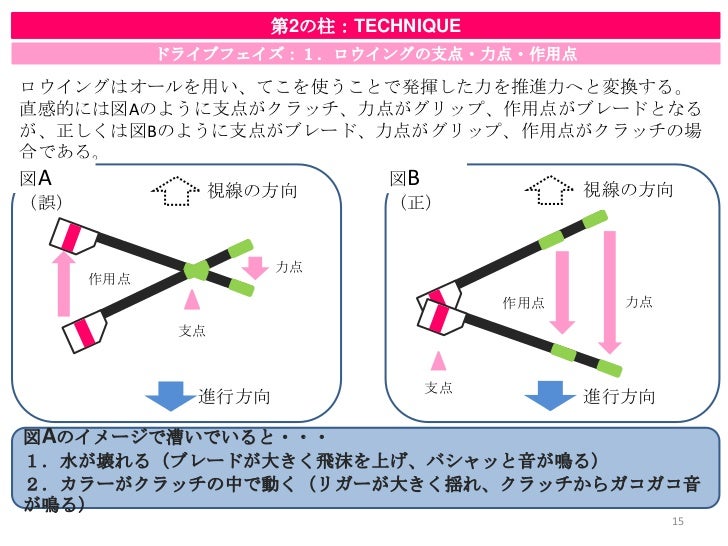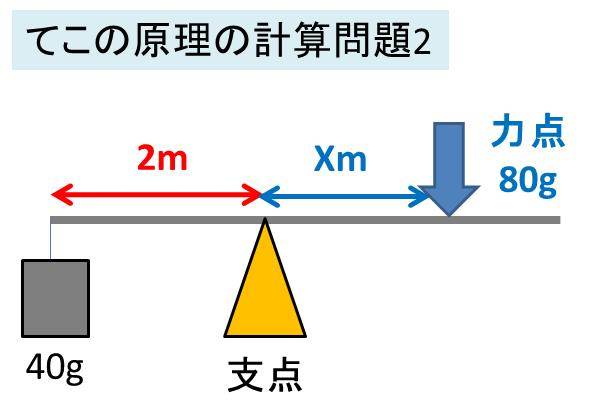 てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |
てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |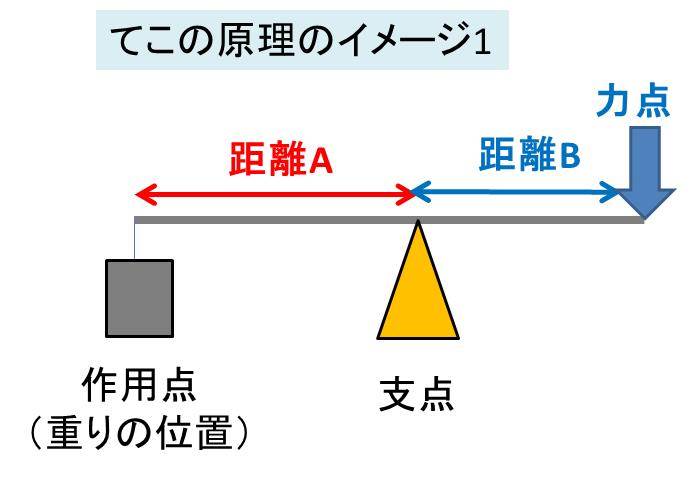
 てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |  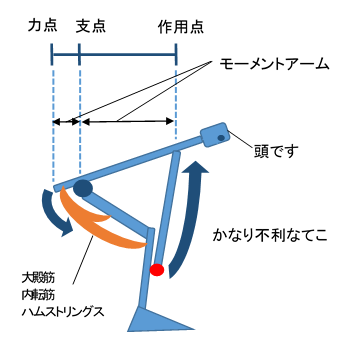てこの原理を用いた計算方法 公式と問題 |
「支点力点作用点 わかりやすく」の画像ギャラリー、詳細は各画像をクリックしてください。
てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |
 てこの原理を用いた計算方法 公式と問題 |  てこの原理を用いた計算方法 公式と問題 |
⑤ てこの原理（支点、力点、作用点）：肘を支点として、てこの原理を応用します。 ⑥ トルクの原理：患者の身体を小さくまとめ、膝を立てて、肩と腰を支えて回転させ、体軸回旋運動を誘発させます。なお、θ の基準位置を変えると、sinθ の部分が cosθ になるので、覚えておいてください。 回転軸から半径 r が伸びる方向に θ の基準をとれば、sinθ ですし、 半径 r の円の接線の方向に θ の基準をとれば、cosθ です。＊ sin(90°θ) = cosθ です。 三角比に慣れてない方は難しいかもしれません。
Incoming Term: 支点力点作用点 わかりやすく, 支点 力点 作用点分かりやすく,
0 件のコメント:
コメントを投稿